hyeori
적응형 선형 뉴런과 학습의 수렴 본문
선형 뉴런 (ADAptive Linear NEuron, ADALINE), 아달린 (Adaline) ← 퍼셉트론의 향상된 버전
아달린은 연속 함수 (continuous function) 으로 비용함수를 정의하고, 최소화하는 핵심 개념을 보여준다. logistic regression, SVM 이해하는데 도움이 된다.
아달린 규칙(위드로우-호프 규칙) vs 퍼셉트론
- 가중치를 업데이트 할 때, 선형활성화 함수를 사용한다.
- 선형 활성화 함수 𝜃(𝑧)는 단순한 항등함수 (identity function)이다.

아달린 알고리즘은 진짜 클래스 레이블과 선형 활성화 함수의 실수 출력 값을 비교하여, 모델의 오차를 계산하고 가중치를 업데이트 한다.
퍼셉트론은 진짜 클래스 레이블과 예측 클래스 레이블을 비교한다.
2.3.1 경사 하강법으로 비용 함수 최소화
지도 학습 알고리즘의 핵심 구성 요소 중 하나, 목적 함수(object function)이다. 최소화하려는 비용함수가 목적함수가 된다.
아달린은 계산된 출력과 진짜 클래스 레이블 사이의 제곱 오차합(SSE)으로 가중치를 학습하기 위한 비용 함수 𝐽를 정의 한다.
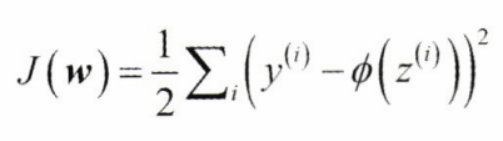
단위 계단 함수 대신 연속적인 선형 활성화 함수 사용 이유 : 비용 함수가 미분 가능해 진다.
볼록함수이다. 경사 하강법(gradient descent)를 사용하여 비용 함수를 최소화하는 가중치를 찾을 수 있다.
각 반복에서 경사의 반대 방향으로 진행한다.
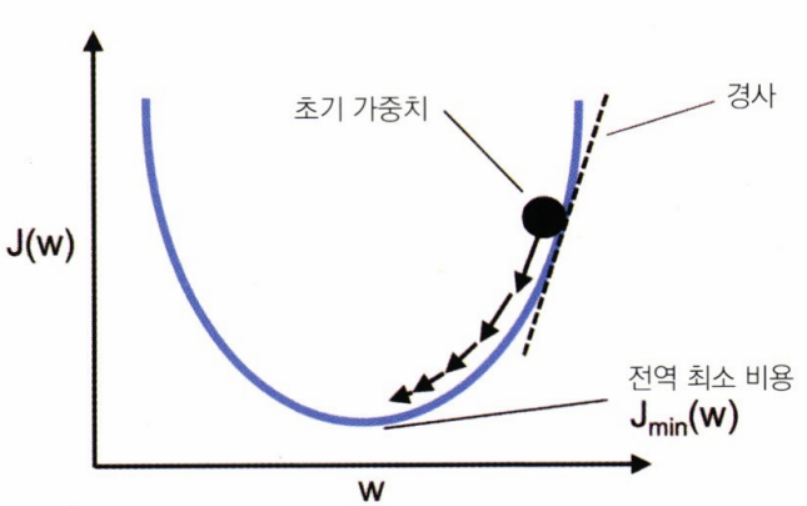
- 경사 하강법을 사용하면 비용 함수 𝐽(𝑤)의 gradient Δ𝐽(𝑤) 반대 방향으로 조금씩 가중치 업데이트 가능

- 가중치 변화량 : 음수의 gradient 에 학습률 𝜂를 곱한 것

- 가중치 업데이트 공식 :

아달린 학습 규칙이 퍼셉트론 규칙과 동일하게 보이지만, 𝜙(𝑧(𝑖))는 정수 클래스 레이블이 아니고 실수이다. 훈련 데이터 셋에 있는 모든 샘플을 기반으로 가중치 업데이트를 계산한다.
→ batch gradient descent 배치 경사 하강법
2.3.2 파이썬으로 아달린 구현
class AdalineGD(object):
"""퍼셉트론 분류기
매개변수
------------
eta : float
학습률 (0.0과 1.0 사이)
n_iter : int
훈련 데이터셋 반복 횟수
random_state : int
가중치 무작위 초기화를 위한 난수 생성기 시드
속성
-----------
w_ : 1d-array
학습된 가중치
errors_ : list
에포크마다 누적된 분류 오류
"""
def __init__(self, eta=0.01, n_iter=50, random_state=1):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
def fit(self, X, y):
"""훈련 데이터 학습
매개변수
----------
X : array-like, shape = [n_samples, n_features]
n_samples개의 샘플과 n_features개의 특성으로 이루어진 훈련 데이터
y : array-like, shape = [n_samples]
타깃값
반환값
-------
self : object
"""
rgen = np.random.RandomState(self.random_state)
self.w_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1]) # 표준편차가 0.01인 정규분포에서 뽑은 랜덤한 작은 수 ,가중치를 m+1 차원으로 초기화 , m : 데이터셋에 있는 features 개수
self.cost_ = []
for i in range(self.n_iter):
net_input = self.net_input(X)
output = self.activation(net_input)
errors = (y- output)
self.w_[1:] += self.eta * X.T.dot(errors) # 가중치 1~m
self.w_[0] += self.eta * errors.sum() # 절편
cost = (errors**2).sum() / 2 # SSE
self.cost_.append(cost)
return self
def net_input(self, X):
"""입력 계산"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, X):
"""선형 활성화 계산"""
return X # 항등함수
def predict(self, X):
"""단위 계단 함수를 사용하여 클래스 레이블을 반환합니다"""
return np.where(self.net_input(X) >= 0.0, 1, -1)
# 두 학습률에서 epoch 횟수 대비 비용 그래프
import matplotlib.pyplot as plt
fig, ax = plt.subplots(nrows = 1, ncols = 2, figsize = (10, 4))
ada1 = AdalineGD(n_iter = 10, eta = 0.01).fit(X,y) # 학습률이 너무 크다, 비용 함수를 최소화하지 못하고, 오차가 epoch마더 점점 커진다<-전역최솟값을 지나쳤기 때문
ax[0].plot(range(1, len(ada1.cost_) +1),
np.log10(ada1.cost_), marker = 'o')
ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('log(Sum-squared_error)')
ax[0].set_title('Adaline - Learning rate 0.01')
ada2 = AdalineGD(n_iter = 10, eta = 0.0001).fit(X,y) # 학습률이 작아서, 전역 최솟값에 수렴하려면 아주 많은 epoch이 필요함.
ax[1].plot(range(1, len(ada2.cost_) +1),
ada2.cost_, marker = 'o')
ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('Sum-squared_error')
ax[1].set_title('Adaline - Learning rate 0.0001')
2.3.3 특정 스케일을 조정하여 경사 하강법 결과 향상
- 표준화 (standardization) 진행
# 특성을 표준화합니다.
X_std = np.copy(X)
X_std[:, 0] = (X[:, 0] - X[:, 0].mean()) / X[:, 0].std()
X_std[:, 1] = (X[:, 1] - X[:, 1].mean()) / X[:, 1].std()
→ 결정 그래프와 비용이 감소되는 그래프 확인 가능
2.3.4 대규모 머신 러닝과 확률적 경사 하강법
𝑁𝑂𝑇𝐸
미니배치 경사 하강법 : 배치 경사 하강법에 비해 가중치 업데이트가 더 자주 일어난다. → 수렴 속도가 더 빠르다. for 반복문을 통해 학습 알고리즘의 계산 효율성이 크게 향상 된다.
class AdalineSGD(object):
"""Adaptive LInear NEuron 분류기
매개변수
------------
eta : float
학습률 (0.0과 1.0 사이)
n_iter : int
훈련 데이터셋 반복 횟수
shuffle : bool (default : True)
true -> 같은 반복이 되지 않도록 epoch 마다 훈련 데이터를 섞음
random_state : int
가중치 무작위 초기화를 위한 난수 생성기 시드
속성
-----------
w_ : 1d-array
학습된 가중치
cost_ : list
모든 훈련 샘플에 대해 epoch마다 누적된 평균 비용 함수의 제곱합
"""
def __init__(self, eta=0.01, n_iter=10,shuffle = True, random_state=None):
self.eta = eta
self.n_iter = n_iter
self.w_initialized = False
self.shuffle = shuffle
self.random_state = random_state
def fit(self, X, y):
"""훈련 데이터 학습
매개변수
----------
X : array-like, shape = [n_samples, n_features]
n_samples개의 샘플과 n_features개의 특성으로 이루어진 훈련 데이터
y : array-like, shape = [n_samples]
타깃 벡터
반환값
-------
self : object
"""
self._initialize_weights(X.shape[1])
self.cost_=[]
for i in range(self.n_iter):
if self.shuffle:
X,y = self._shuffle(X,y)
cost = []
for xi, target in zip(X,y):
cost.append(self._update_weights(xi, target))
avg_cost = sum(cost)/ len(y)
self.cost_.append(avg_cost)
return self
def partial_fit(self,X,y):
"""가중치를 다시 초기화하지 않고 훈련 데이터를 학습합니다"""
if not self.w_initialized:
self._initialize_weights(X.shape[1])
if y.ravel().shape[0] > 1:
for xi, target in zip(X,y):
self._update_weights(xi, target)
else:
self._update_weights(X,y)
return self
def _shuffle(self, X, y):
"""훈련 데이터를 섞습니다"""
r = self.rgen.permutation(len(y))
return X[r], y[r]
def _initialize_weights(self,m) :
"""랜덤한 작은 수로 가중치를 초기화합니다"""
self.rgen = np.random.RandomState(self.random_state)
self.w_ = self.rgen.normal(loc = 0.0, scale = 0.01, size = 1 + m)
self.w_initialized = True
def _update_weights(self, xi, target):
"""아달린 학습 규칙을 적용하여 가중치를 업데이트합니다"""
output = self.activation(self.net_input(xi))
error = (target - output)
self.w_[1:] += self.eta * xi.dot(error)
self.w_[0] += self.eta * error
cost = 0.5 * error**2
return cost
def net_input(self, X):
"""최종 입력 계산"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, X):
"""선형 활성화 계산"""
return X # 항등함수
def predict(self, X):
"""단위 계단 함수를 사용하여 클래스 레이블을 반환합니다"""
return np.where(self.net_input(X) >= 0.0, 1, -1)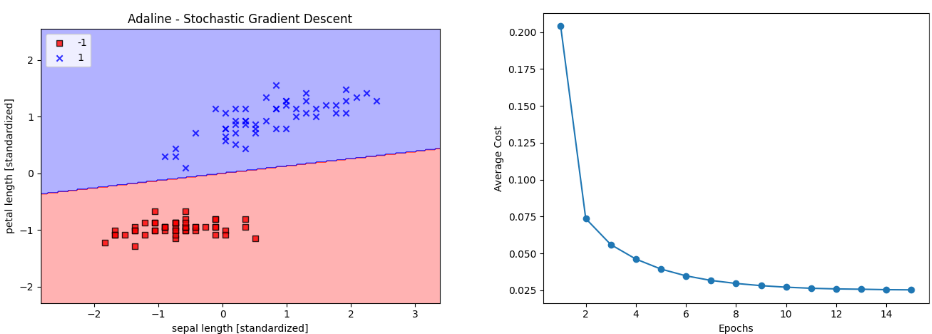
평균 비용이 상당히 빠르게 감소, 스트리밍 데이터를 사용하는 온라인 학습 방식으로 모델을 훈련하려면 개개의 sample마다 partial_fit 메서드 호출
'머신러닝' 카테고리의 다른 글
| 범주형 데이터 다루기 (0) | 2024.05.08 |
|---|---|
| 누락된 데이터 다루기 (0) | 2024.05.08 |
| 파이썬으로 퍼셉트론 학습 알고리즘 구현 (0) | 2024.05.08 |
| 인공 뉴런 : 초기 머신 러닝의 간단한 역사 (1) | 2024.05.08 |
| 03) 분할 정복 : 규칙 기반의 분류 (1) | 2024.02.20 |




