hyeori
유용한 특성 선택 본문
- 과대적합(overfitting) : 모델이 테스트 데이터셋보다 훈련 데이터셋에서 성능이 훨씬 높다.
→ 더 많은 훈련 데이터
→ 규제를 통해 복잡도를 제한
→ 파라미터 개수가 적은 간단한 모델 선택
→ 데이터 차원을 줄이기
4.5.1 모델 복잡도 제한을 위한 L1 규제와 L2 규제
- L2 규제 (Ridge) :
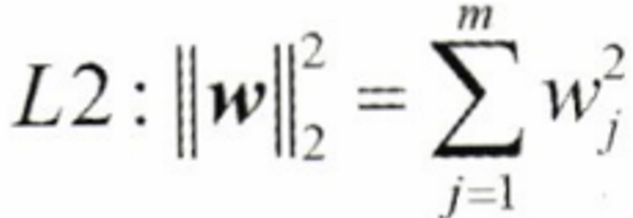
- L1 규제 (Lasso) :
가중치 제곱 → 가중치 절댓값, 희소한 특성 벡터를 만든다. 대부분의 특성 가중치가 0이 된다.(고차원 데이터의 경우), 훈련 샘플보다 관련 없는 특성이 더 많은 경우

4.5.2 L2 규제의 기하학적 해석
L2 규제 ) 비용함수 + 패널티 항
목표 : train data에서 비용함수를 최소화하는 가중치 값의 조합을 찾자! (타원 중심 포인트)

4.5.3 L1 규제를 사용한 희소성

- C 가 커질수록 규제가 풀린다. C = 1/lambda

4.5.4 순차 특성 선택 알고리즘
일부만 선택
- 전진선택법
- 후진선택법
차원 축소 기법
- 특성 선택 (feature selection)
- 특성 추출 (feature extraction)
- 순차 후진 선택 (Sequential Backward Selection, SBS)
- 전체 특성에서 순차적으로 특성 제거
# 주요 코드
while dim > self.k_features:
scores = []
subsets = []
for p in combinations(self.indices_, r=dim - 1):
score = self._calc_score(X_train, y_train,
X_test, y_test, p)
scores.append(score)
subsets.append(p)
best = np.argmax(scores) # 점수 최대값
self.indices_ = subsets[best] # index 넣기
self.subsets_.append(self.indices_)
dim -= 1
self.scores_.append(scores[best]) # 최적 조합의 정확도 점수를 리스트에 모은다.
self.k_score_ = self.scores_[-1]
return self'머신러닝' 카테고리의 다른 글
| 랜덤 포레스트의 특성 중요도 사용 (0) | 2024.05.08 |
|---|---|
| 특성 스케일 맞추기 (0) | 2024.05.08 |
| 데이터셋을 훈련 데이터셋과 테스트 데이터 셋으로 나누기 (0) | 2024.05.08 |
| 범주형 데이터 다루기 (0) | 2024.05.08 |
| 누락된 데이터 다루기 (0) | 2024.05.08 |



