hyeori
02) 분할 정복 : 의사 결정 트리 본문
단순한 선택 과정을 거쳐 복잡한 결정을 한다.
| 의사 결정 트리의 이해
* 루트노드 (root node)
* 결정 노드 (decision node)
* 분기 (branches)
* 잎 노드 (terminal node, leaf node, 일련의 결정이 이뤄진 결과로 수행할 액션 나타냄)
장점)
사람이 읽을 수 있는 형식
어떻게, 왜 특정 작업에 잘 작동하는지 혹은 잘 작동하지 않는지에 대한 통찰력 제공
결정이 많아질 경우 복잡해지며, 의사 결정 트리가 데이터에 과적합되는 경향 갖게 됨
| 분할 정복
재귀분할(recursiving) 이라고 불리는 휴리스틱 사용 → 분할 정복(divide and conquer)
처음에 루트노드는 분할이 일어나지 않았기 때문에 전체 데이터 셋을 표현하고 있다.
이상적으로 타깃 클래스를 가장 잘 예측하는 특징 선택한다.
각 분기별로 처리 후 알고리즘은 종료 기준에 도달할 때까지 데이터를 분할하고 정복한다.
결정 노드를 생성할 떄 마다 최고의 후보 특징을 선택한다.
분할 정복이 멈출 때
ㅁ 노드에 있는 모든 예시가 같은 클래스를 가진다
ㅁ 예시를 구별하는 특징이 남아있지 않다.
ㅁ 미리 정의된 크기 한도까지 트리가 자랐다.
작은 파티션으로 들어가 정확히 분류될 때까지 점차 세부적인 특징들로 데이터를 나눔으로써 분할 정복을 이어나갈 수 있다. 하지만 이런 방식으로 의사 결정 트리를 과적합시키는 것은 바람직 하지 않다.
각 그룹에 80% 이상의 예시가 단일 클래스 이기 때문에 알고리즘은 중단하고 과적합 문제를 피해야 한다.
이것이 종료 기준의 기초를 형성한다.
[TIP]
대각선이 데이터를 더 깔끔하게 분리할 수 있다는 것을 인식했을 것이다. 의사 결정 트리는 축 평행 분할(axis-parallel splits)을 사용하기 때문에 지식을 표하는 데 한계가 있다. 분할이 한 번에 하나의 특징만을 고려하기 때문에 의사 결정 트리는 더 복잡한 결정 경계를 형성하지 못한다.
| C5.0 의사 결정 트리 알고리즘
의사 결정 트리의 수많은 구현 중 가장 잘 알려진 구현이다.
장점)
- 많은 유형의 문제에 잘 실행되는 범용 분류기다.
- 수치 특징, 명목 특징, 누락 데이터를 다룰 수 있는 고도로 자동화된 학습 과정이다.
- 중요하지 않은 특징은 제외한다.
- 작은 데이터셋과 큰 데이터 셋에 모두 사용 될 수 있다.
- 상대적으로 작은 트리에 대해 수학적 배경 없이 해석될 수 있는 모델을 만든다.
- 다른 복잡한 모델보다 더 효율적이다.
단점)
- 의사 결정 트리 모델이 레벨 수가 많은 특징의 분할로 편향될 수 있다.
- 모델이 과적합 또는 과소적합되기 싶다.
- 축 평행 분할에 의존하기 때문에 어떤 관계는 모델리이 어려울 수 있다.
- 훈련 데이터에서 작은 변화가 결정 로직에 큰 변화를 초래할 수 있다.
- 큰 트리는 해석이 어렵고 트리가 만든 결정은 직관적이지 않아 보일 수 있다.
| 최고의 분할 선택
첫 번째 문제 :
분할 조건이 되는 특징 식별하는 것
순도(purity) :
예시의 부분 집합이 단일 클래스를 포함하는 정도, 단일 클래스로 이뤄진 부분집합을 순수하다고 한다.
엔트로피(entropy) :
순도 측정법, 클래스 값의 집합 내에서 무작위성(randomness)나 무질서(disorder)를 정량화 한다.
비트(bits) 단위로 측정된다. 가능한 클래스가 2개 뿐인 경우 엔트로피 값의 범위는 0에서 1이다.
클래스가 n인 경우 엔트로피의 범위는 0에서 log(n)이다. 가가각의 경우에 최솟값은 샘플이 완전히 동질적임을 나타내는 반면 최댓갑은 데이터가 가능한 한 다양하고 어떤 그룹도 작은 복수성르 갖지 않음을 나타낸다.
c : 클래스의 레벨 수, p_i : 클래스 레벨 i에 속하는 값의 비율
ex) 빨간색 60%, 흰색 40% 두 클래스를 갖는 데이터 파티션이 있다고 하자. 엔트로피는 다음과 같이 계산 할 수 있다.

curve() 함수를 이용해 가능한 모든 x 값에 대해 엔트로피를 그릴 수 있다.


엔트로피의 최고치가 x=0.5에서 보이는 것처럼 50-50분할은 엔트로피를 최대로 만든다. 한 클래스가 다른 클래스에 대해 점점 더 우세할수록 엔트로피는 0으로 줄어든다.
정보 획득량(information gain) : 각 특징별로 분할로 인해 생긱는 동질성의 변활를 계산
파티션에 소속된 모든 레코드의 비율에 따라 각 파티션의 엔트로피에 가중치를 부여한다. 이는 다음 공식으로 기술할 수 있다.
분할로 생기는 전체 엔트로피는 n개 파티션에 대해 파티션에 속하는 예시 비율(w_i) 로 각 파티션의 엔트로피에 가중치를 부여해 합산한 것이다.
정보 획득량이 높을 수록 이 특징에 대해 분할한 후 동질적 그룹을 생성하기에 더 좋은 특징이다. 정보 획득량이 0인 경우 이 특징에 대해 분할을 하면 엔트로피가 감소하지 않는다. 반면 최대 정보 획득량의 경우 분할 전의 엔트로피와 정보 획득량이 동일하다. 이는 분할 후 엔트로피가 0이라는 것을 의미하며, 분할로 인해 완전히 동질적인 그룹이 만들어졌음을 의미한다.
의사결정 트리는 엔트로피를 줄이는 분할을 찾고 궁극적으로 그룹 내의 동질성을 증가시키려고 한다.
| 의사 결정 트리 가지치기
가지치기(pruning) 과정은 처음 보는 데이터에 일반화가 잘되도록 트리의 크기를 줄이는 것이다.
이 문제의 해결책 중 하나는
결정이 특정 개수에 도달하거나 결정 노드가 포함하는 예시 개수가 아주 작은 숫ㄱ자가 되면 트리의 성장을 멈추게 하는 것이다.
조기종료(early stopping), 사전 가지치기(pre-pruning)
위 방법은 트리가 불필요한 일을 하지 않게 해주므로 설득력 있는 전략이다.
이 방식의 단점은 트리가 크게 자랐다면 학습할 수도 있는 중요한 패턴을 놓치는지 알 방법이 엇다는 점이다.
대안으로 사후 가지치기(post-pruning)은 의도적으로 트리를 아주 크게 자라게 한 후 트리 크기를 좀 더 적절한 수준으로 줄이고자 잎 노드를 자른다.
C5.0 알고리즘의 장점 중 하나는 가지치기를 고집한다는 것이다. 이알고리즘의 전반적인 전략은 트리를 사후 가지 치기하는 것이다. 먼저 훈련 데이터에 과적합되는 큰 트리로 자라게 한다. 나중에 분류 오류에 영향이 거의 없는 노드와 분기는 제거한다.
하위 트리 올리기(subtree raising), 하위 트리 대체(subtree replacement) :
어떤 경우에는 전체 분기가 트리의 위쪽으로 옮겨지거나 좀 더 간단한 의사 결정으로 대체된다.
| 예제: C5.0 의사 결정 트리를 이용한 위험 은행 대출 식별
의사 결정 트리는 은행 업계에서 너리 사용되고 있다. 다출 거절 유무에 따라 경영진은 그 사유를 설명할 수 있어야 한다.
| 1단계 : 데이터 수집
| 2단계 : 데이터 탐색과 준비

1000개의 관측치와 17개의 특징이 보이며, 특징은 팩터 데이터 타입과 정수 데이터 타입이 함께 있다.
채무 불이행을 예측할 것 같은 일부 대출 특징에 대해 table() 출력을 살펴보자. 신청자의 수표 계좌 잔고와 저축 계좌 잔고가 범주형 변수로 저장돼 있다.

수표 계좌 잔고와 저축 계좌 잔고는 대출 채무 불이행 상태의 중요한 예측 변수가 될 수 있다.

기한 ) 4개월 ~ 72개월, 대출금) 250DM ~ 18420DM
default 벡터는 대출 신청자가 합의된 금액을 상환했는지 아니면 지불 조건을 맞출 수 없어 채무 불이행이 됐는지 나타낸다.

| 데이터 준비 : 랜덤한 훈련 및 테스트 데이터셋 생성
의사 결정 트리를 만들기 위한 훈련 데이터셋과 새로운 데이터에 대해 모델 성능을 평가하기 위한 테스트 데이터셋 두 부분으로 데이터를 분리한다.
훈련) 90%, 테스트) 10%

훈련 및 테스트 데이터셋에서 대출 디폴트와 유사한 분포를 보이므로 이제 결정 트리를 구축할 수 있다.
| 3단계 : 데이터로 모델 훈련
credit_train의 17번째 열은 default 클래스 변수이므로, 이 변수를 훈련 데이터 프레임에서 제외하고 분류를 하기 위한 목표 벡터로 제공해야한다.

C5.0 함수는 factor 을 요구한다. 따라서 credit_trains$defalut 를 factor 로 바꿔준다.

트리에 대한 간단한 사실을 일부 보여준다.
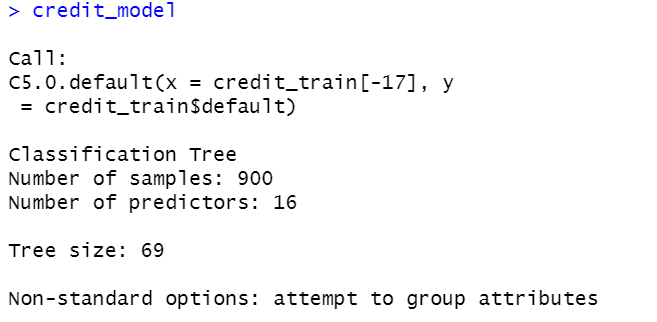
트리를 생성했던 함수 호출과 특징 개수, 트리를 자라게 하는 데 사용 된 예시 개수를 포함한다. 트리 크기는 57로, 트리가 57개의 결정으로 이뤄진 깊이라는 것을 나타낸다.
트리의 결정을 보려면 모델에 대한 summary() 함수를 호출하면 된다.

혼동 행렬(confusion matrix) :
모델이 훈련 데이터에서 부정확하게 분류한 레코드를 보여주는 교차표다.

Errors 헤딩은 모델이 11.0 %의 오류율로 900개의 훈련 인스턴스 중 99개를 제외하고 전부 정화하게 분류했음을 알려준다. 10개의 실제 no 값은 yes로 부정확하게 분류(FP : 거짓 긍정)된 반면, 89개의 yes 값은 no로 오분류(FN : 거짓 부정)됐다.
의사 결정 트리는 모델을 훈련 데이터에 과적합시키는 경향이 있다. 따라서 테스트 데이터셋에 대해 의사 결정 트리를 계속해서 평가하는 것이 특히 중요하다.
| 4단계: 모델 성능 평가

위 명령은 예측된 클래스 값 벡터를 생성한다. gmodels 패키지에 있는 CrossTable(함수)를 이용해 이 벡터와 실제 클래스 값을 비교할수 있다. prop.c 와 prop.r 파라미터를 FALSE로 설정 하면 표에서 열과 행 비율을 제거한다. 남은 백분율 prop.t는 전체 레코트 개수에서 셀의 레코드 비율을 나타낸다.

prop.c, r 의 설정을 default 값으로 뒀다.

정확도는 55+15=70 으로 70% 이며, 오류율은 30% 이다.
| 5단게 : 모델 성능개선
- 의사 결정 트리의 정확도 향상
적응향 부스팅(adaptive boosting, 에이다부스트 AdaBoost)을 추가한 것이다. 이 방법은 여러 개의 의사 결정 트리를 만들어서 각 예시에 대해 최고 클래스를 투표하게 만드는 과정이다.
부스팅은 성능이 약한 여러 학습자를 결합함으로써 어느 하나의 학습자 혼자보다 훨씬 강한 팀을 만들 수 있다는 생각에 뿌리를 두고 있다.
부스팅 팀에 사용할 독립적인 의사 결정 트리의 개수를 나타내는trials 파라미터를 추가한다. trials 파라미터는 상한 선을 설정한다. 추가 시행이 정확도를 향상 시키지 못할 것으로 보이면 알고리즘은 더 이상 트리를 추가하지 않는다.
10회 시행으로 시작해보자.


오류률이 0.014%로 개선되었다.


30%의 오류율, 채무 불이행은 18/35 으로 51% 만 정확히 예측한다. 아마도 상대적으로 작은 훈련 데이터셋과 함수 관계에 이거나, 이 문제가 원래 해결하기 매우 어려운 문제이기 때문일 수 있다.
부스팅이 모든 의사 결정 트리에 기본으로 적용되지 않는 이유)
- 의사 결정 트리를 한 번 만드는 데 계산 시간이 많이 걸린다면, 여러 개의 트리를 만들면 계산적으로 비현실적일 수 있다.
- 훈련 데이터에 노이즈가 많으면 부스팅으로 전혀 개선되지 않을 수 있다.
- 다른 것보다 더 비싼 실수
거짓 부정 개수를 줄일 수 있는 방안 중 하나는 여러 오류 유형에 페널티를 주는 것이다.
페널티는 비용 행렬(cost matrix)에 지정되며, 각 오류가 다른 이에 비해 몇 배나 비용이 많이 드는지를 명시한다.
비용 행렬을 구성 후, 차원 지정
예측된 값과 실제 값 모두 yes 나 no 두 값을 갖기 때문에 이 두값으로 이뤄진 두 벡터의 리스트를 이용해 2x2 행렬을 기술한다. 이와 함께 이후의 혼란을 피하고자 행렬의 차원에 이름을 지정한다.


거짓 부정은 거짓 긍정의 비용 1에 대해 비용 4를 갖는다. 은행은 채무 불이행으로 놓친 기회이 4배만큼 비용이 드는 것으로 생각한다고 가정해보자. 비용행렬이 분류에 어떻게 영향을 주는지 확인하고자 C5.0O 함수의 costs 파라미터를 이용해서 의사 결정 트리에 적용해보자.


채무 불이행의 28/35로 80%가 채무 불이행한 것으로 정확히 예측했다.
'머신러닝' 카테고리의 다른 글
| 적응형 선형 뉴런과 학습의 수렴 (0) | 2024.05.08 |
|---|---|
| 파이썬으로 퍼셉트론 학습 알고리즘 구현 (0) | 2024.05.08 |
| 인공 뉴런 : 초기 머신 러닝의 간단한 역사 (1) | 2024.05.08 |
| 03) 분할 정복 : 규칙 기반의 분류 (1) | 2024.02.20 |
| 01) 머신러닝 소개 (0) | 2024.02.20 |



